A key theme in real analysis is that of studying general functions {f: X \rightarrow {\bf R}} or {f: X \rightarrow {\bf C}} by first approximating them by "simpler" or "nicer" functions. But the precise class of "simple" or "nice" functions may vary from context to context. In measure theory, for instance, it is common to approximate measurable functions by indicator functions or simple functions. But in other parts of analysis, it is often more convenient to approximate rough functions by continuous or smooth functions (perhaps with compact support, or some other decay condition), or by functions in some algebraic class, such as the class of polynomials or trigonometric polynomials.

In order to approximate rough functions by more continuous ones, one of course needs tools that can generate continuous functions with some specified behaviour. The two basic tools for this are Urysohn's lemma, which approximates indicator functions by continuous functions, and the Tietze extension theorem, which extends continuous functions on a subdomain to continuous functions on a larger domain. An important consequence of these theorems is the Riesz representation theorem for linear functionals on the space of compactly supported continuous functions, which describes such functionals in terms of Radon measures.

Sometimes, approximation by continuous functions is not enough; one must approximate continuous functions in turn by an even smoother class of functions. A useful tool in this regard is the Stone-Weierstrass theorem, that generalises the classical Weierstrass approximation theorem to more general algebras of functions.

As an application of this theory (and of many of the results accumulated in previous lecture notes), we will present (in an optional section) the commutative Gelfand-Neimark theorem classifying all commutative unital {C^*}-algebras.

— 1. Urysohn's lemma —

Let {X} be a topological space. An indicator function {1_E} in this space will not typically be a continuous function (indeed, if {X} is connected, this only happens when {E} is the empty set or the whole set). Nevertheless, for certain topological spaces, it is possible to approximate an indicator function by a continuous function, as follows.

Lemma 1 (Urysohn's lemma) Let {X} be a topological space. Then the following are equivalent:

A topological space which obeys any (and hence all) of (i-iv) is known as a normal space; definition (i) is traditionally taken to be the standard definition of normality. We will give some examples of normal spaces shortly.

Proof: The equivalence of (iii) and (iv) is clear, as the complement of a closed set is an open set and vice versa. The equivalence of (i) and (ii) follows similarly.

To deduce (i) from (iii), let {K, L} be disjoint closed sets, let {f} be as in (iii), and let {U, V} be the open sets {U := \{ x \in X: f(x) > 2/3 \}} and {V := \{x \in X: f(x) < 1/3 \}}.

The only remaining task is to deduce (iv) from (ii). Suppose we have a closed set {K = K_1} and an open set {U = U_0} with {K_1 \subset U_0}. Applying (ii), we can find an open set {U_{1/2}} and a closed set {K_{1/2}} such that

\displaystyle K_1 \subset U_{1/2} \subset K_{1/2} \subset U_0.

Applying (ii) two more times, we can find more open sets {U_{1/4}, U_{3/4}} and closed sets {K_{1/4}, K_{3/4}} such that

\displaystyle K_1 \subset U_{3/4} \subset K_{3/4} \subset U_{1/2} \subset K_{1/2} \subset U_{1/4} \subset K_{1/4} \subset U_0.

Iterating this process, we can construct open sets {U_q} and closed sets {K_q} for every dyadic rational {q = a/2^n} in {(0,1)} such that {U_q \subset K_q} for all {0 < q < 1}, and {K_{q'} \subset U_{q}} for any {0 \leq q < q' \leq 1}.

If we now define {f(x) := \sup \{ q: x \in U_q \} = \inf \{ q: x \not \in K_q \}}, where {q} ranges over dyadic rationals between {0} and {1}, and with the convention that the empty set has sup {0} and inf {1}, one easily verifies that the sets {\{ f(x) > \alpha \} = \bigcup_{q>\alpha} U_q} and {\{f(x) < \alpha\} = \bigcup_{q<\alpha} X \backslash K_q} are open for every real number {\alpha}, and so {f} is continuous as required. \Box

The definition of normality is very similar to the Hausdorff property, which separates pairs of points instead of closed sets. Indeed, if every point in {X} is closed (a property known as the {T_1} property), then normality clearly implies the Hausdorff property. The converse is not always true, but (as the term suggests) in practice most topological spaces one works with in real analysis are normal. For instance:

Exercise 1 Show that every metric space is normal.

Exercise 2 Let {X} be a Hausdorff space.

Exercise 3 Let {{\bf R}} be the real line with the usual topology {{\mathcal F}}, and let {{\mathcal F}'} be the topology on {{\bf R}} generated by {{\mathcal F}} and the set {\{{\bf Q}\}} consisting only of the rationals {{\bf Q}}; in other words, {{\mathcal F}'} is the coarsest refinement of the usual topology that makes the set of rationals {{\bf Q}} an open set. Show that {({\bf R}, {\mathcal F}')} is Hausdorff, with every point closed, but is not normal.

The above example was a simple but somewhat artificial example of a non-normal space. One can create more "natural" examples of non-normal Hausdorff spaces (with every point closed), but establishing non-normality becomes more difficult. The following example is due to Stone.

Exercise 4 Let {{\bf N}^{\bf R}} be the space of natural number-valued tuples {(n_x)_{x \in {\bf R}}}, endowed with the product topology (i.e. the topology of pointwise convergence).

The property of being normal is a topological one, thus if one topological space is normal, then any other topological space homeomorphic to it is also normal. However, (unlike, say, the Hausdorff property), the property of being normal is not preserved under passage to subspaces:

Exercise 5 Given an example of a subspace of a normal space which is not normal. (Hint: use Exercise 4, possibly after replacing {{\bf R}} with a homeomorphic equivalent.)

Let {C_c(X \rightarrow {\bf R})} be the space of real continuous compactly supported functions on {X}. Urysohn's lemma generates a large number of useful elements of {C_c(X \rightarrow {\bf R})}, in the case when {X} is locally compact Hausdorff:

Exercise 6 Let {X} be a locally compact Hausdorff space, let {K} be a compact set, and let {U} be an open neighbourhood of {K}. Show that there exists {f \in C_c(X \rightarrow {\bf R})} such that {1_K(x) \leq f(x) \leq 1_U(x)} for all {x \in X}. (Hint: First use the local compactness of {X} to find a neighbourhood of {K} with compact closure; then restrict {U} to this neighbourhood. The closure of {U} is now a compact set; restrict everything to this set, at which point the space becomes normal.)

One consequence of this exercise is that {C_c(X \rightarrow {\bf R})} tends to be dense in many other function spaces. We give an important example here:

Definition 2 (Radon measure) Let {X} be a locally compact Hausdorff space that is also {\sigma}-compact, and let {{\mathcal B}} be the Borel {\sigma}-algebra. An (unsigned) Radon measure is a unsigned measure {\mu: {\mathcal B} \rightarrow {\bf R}^+} with the following properties:

Example 1 Lebesgue measure {m} on {{\bf R}^n} is a Radon measure, as is any absolutely continuous unsigned measure {m_f}, where {f \in L^1({\bf R}^n, dm)}. More generally, if {\mu} is Radon and {\nu} is a finite unsigned measure which is absolutely continuous with respect to {\mu}, then {\nu} is Radon. On the other hand, counting measure on {{\bf R}^n} is not Radon (it is not locally finite). It is possible to define Radon measures on Hausdorff spaces that are not {\sigma}-compact or locally compact, but the theory is more subtle and will not be considered here. We will study Radon measures more thoroughly in the next section.

Proposition 3 Let {X} be a locally compact Hausdorff space that is also {\sigma}-compact, and let {\mu} be a Radon measure on {X}. Then for any {0 < p < \infty}, {C_c(X \rightarrow {\bf R})} is a dense subset in (real-valued) {L^p(X,\mu)}. In other words, every element of {L^p(X,\mu)} can be expressed as a limit (in {L^p(X,\mu)}) of continuous functions of compact support.

Proof: Since continuous functions of compact support are bounded, and compact sets have finite measure, we see that {C_c(X)} is a subspace of {L^p(X,\mu)}. We need to show that the closure {\overline{C_c(X)}} of this space contains all of {L^p(X,\mu)}.

Let {E} be a Borel set of finite measure. Applying inner and outer regularity, we can find a sequence of compact sets {K_n \subset E} and open sets {U_n \supset E} such that {\mu(E \backslash K_n), \mu(U_n \backslash E) \rightarrow 0}. Applying Exercise 6, we can then find {f_n \in C_c(X \rightarrow {\bf R})} such that {1_{K_n}(x) \leq f_n(x) \leq 1_{U_n}(x)}. In particular, this implies (by the squeeze theorem) that {f_n} converges in {L^p(X,\mu)} to {1_E} (here we use the finiteness of {p}); thus {1_E} lies in {\overline{C_c(X \rightarrow {\bf R})}} for any measurable set {E}. By linearity, all simple functions lie in {\overline{C_c(X \rightarrow {\bf R})}}; taking closures, we see that any {L^p} function lies in {\overline{C_c(X \rightarrow {\bf R})}}, as desired. \Box

Of course, the real-valued version of the above proposition immediately implies a complex-valued analogue. On the other hand, the claim fails when {p=\infty}:

Exercise 7 Let {X} be a locally compact Hausdorff space that is {\sigma}-compact, and let {\mu} be a Radon measure. Show that the closure of {C_c(X \rightarrow {\bf R})} in {L^\infty(X,\mu)} is {C_0(X \rightarrow {\bf R})}, the space of continuous real-valued functions which vanish at infinity (i.e. for every {\varepsilon > 0} there exists a compact set {K} such that {|f(x)| \leq \varepsilon} for all {x \not \in K}). Thus, in general, {C_c(X \rightarrow {\bf R})} is not dense in {L^\infty(X,\mu)}.

Thus we see that the {L^\infty} norm is strong enough to preserve continuity in the limit, whereas the {L^p} norms are (locally) weaker and permit discontinuous functions to be approximated by continuous ones.

Another important consequence of Urysohn's lemma is the Tietze extension theorem:

Theorem 4 (Tietze extension theorem) Let {X} be a normal topological space, let {[a,b] \subset {\bf R}} be a bounded interval, let {K} be a closed subset of {X}, and let {f: K \rightarrow [a,b]} be a continuous function. Then there exists a continuous function {\tilde f: X \rightarrow [a,b]} which extends {f}, i.e. {\tilde f(x) = f(x)} for all {x \in K}.

Proof: It suffices to find an continuous extension {\tilde f: X \rightarrow {\bf R}} taking values in the real line rather than in {[a,b]}, since one can then replace {\tilde f} by {\min(\max(\tilde f, a),b)} (note that min and max are continuous operations).

Let {T: BC(X \rightarrow {\bf R}) \rightarrow BC(K \rightarrow {\bf R})} be the restriction map {Tf := f\downharpoonright_K}. This is clearly a continuous linear map; our task is to show that it is surjective, i.e. to find a solution to the equation {Tg=f} for each {f \in BC(X \rightarrow {\bf R})}. We do this by the standard analysis trick of getting an approximate solution to {Tg=f} first, and then using iteration to boost the approximate solution to an exact solution.

Let {f: K \rightarrow {\bf R}} have sup norm {1}, thus {f} takes values in {[-1,1]}. To solve the problem {Tg=f}, we approximate {f} by {\frac{1}{3} 1_{f\geq 1/3} - \frac{1}{3} 1_{f \leq -1/3}}. By Urysohn's lemma, we can find a continuous function {g: X \rightarrow [-1/3,1/3]} such that {g=1/3} on the closed set {\{ x \in K: f \geq 1/3\}} and {g=-1/3} on the closed set {\{ x \in K: f \leq -1/3\}}. Now, {Tg} is not quite equal to {f}; but observe from construction that {f-Tg} has sup norm {2/3}.

Scaling this fact, we conclude that, given any {f \in BC(K \rightarrow {\bf R})}, we can find a decomposition {f = Tg + f'}, where {\|g\|_{BC(X \rightarrow {\bf R})} \leq \frac{1}{3} \| f \|_{BC(K \rightarrow {\bf R})}} and {\|f'\|_{BC(K \rightarrow {\bf R})} \leq \frac{2}{3} \|f\|_{BC(K \rightarrow {\bf R})}}.

Starting with any {f=f_0 \in BC(K \rightarrow {\bf R})}, we can now iterate this construction to express {f_n = Tg_n + f_{n+1}} for all {n =0,1,2,\ldots}, where {\|f_n\|_{BC(K \rightarrow R)} \leq (\frac{2}{3})^n \|f\|_{BC(K \rightarrow {\bf R})}} and {\|g_n\|_{BC(X \rightarrow {\bf R})} \leq \frac{1}{3} (\frac{2}{3})^n \|f\|_{BC(K \rightarrow {\bf R})}}. As {BC(X \rightarrow {\bf R})} is a Banach space, we see that {\sum_{n=0}^\infty g_n} converges absolutely to some limit {g \in BC(X \rightarrow {\bf R})}, and that {Tg=f}, as desired. \Box

Remark 1 Observe that Urysohn's lemma can be viewed the special case of the Tietze extension theorem when {K} is the union of two disjoint closed sets, and {f} is equal to {1} on one of these sets and equal to {0} on the other.

Remark 2 One can extend the Tietze extension theorem to finite-dimensional vector spaces: if {K} is a closed subset of a normal vector space {X} and {f: K \rightarrow {\bf R}^n} is bounded and continuous, then one has a bounded continuous extension {\overline{f}: K \rightarrow {\bf R}^n}. Indeed, one simply applies the Tietze extension theorem to each component of {f} separately. However, if the range space is replaced by a space with a non-trivial topology, then there can be topological obstructions to continuous extension. For instance, a map {f: \{0,1\} \rightarrow Y} from a two-point set into a topological space {Y} is always continuous, but can be extended to a continuous map {\tilde f: {\bf R} \rightarrow Y} if and only if {f(0)} and {f(1)} lie in the same path-connected component of {Y}. Similarly, if {f: S^1 \rightarrow Y} is a map from the unit circle into a topological space {Y}, then a continuous extension from {S^1} to {{\bf R}^2} exists if and only if the closed curve {f: S^1 \rightarrow Y} is contractible to a point in {Y}. These sorts of questions require the machinery of algebraic topology to answer them properly, and are beyond the scope of this course.

There are analogues for the Tietze extension theorem in some other categories of functions. For instance, in the Lipschitz category, we have

Exercise 8 Let {X} be a metric space, let {K} be a subset of {X}, and let {f: K \rightarrow {\bf R}} be a Lipschitz continuous map with some Lipschitz constant {A} (thus {|f(x)-f(y)| \leq A d(x,y)} for all {x,y \in K}). Show that there exists an extension {\tilde f: X \rightarrow {\bf R}} of {f} which is Lipschitz continuous with the same Lipschitz constant {A}. (Hint: A "greedy" algorithm will work here: pick {\tilde f} to be as large as one can get away with (or as small as one can get away with.))

One can also remove the requirement that the function {f} be bounded in the Tietze extension theorem:

Exercise 9 Let {X} be a normal topological space, let {K} be a closed subset of {X}, and let {f: K \rightarrow {\bf R}} be a continuous map (not necessarily bounded). Then there exists an extension {\tilde f: X \rightarrow {\bf R}} of {f} which is still continuous. (Hint: first "compress" {f} to be bounded by working with, say, {\arctan(f)} (other choices are possible), and apply the usual Tietze extension theorem. There will be some sets in which one cannot invert the compression function, but one can deal with this by a further appeal to Urysohn's lemma to damp the extension out on such sets.)

There is also a locally compact Hausdorff version of the Tietze extension theorem:

Exercise 10 Let {X} be locally compact Hausdorff, let {K} be compact, and let {f \in C(K \rightarrow {\bf R})}. Then there exists {\tilde f \in C_c(X \rightarrow {\bf R})} which extends {f}.

Proposition 3 shows that measurable functions in {L^p} can be approximated by continuous functions of compact support (cf. Littlewood's second principle). Another approximation result in a similar spirit is Lusin's theorem:

Theorem 5 (Lusin's theorem) Let {X} be a locally compact Hausdorff space that is {\sigma}-compact, and let {\mu} be a Radon measure. Let {f: X \rightarrow {\bf R}} be a measurable function supported on a set of finite measure, and let {\varepsilon > 0}. Then there exists {g \in C_c(X \rightarrow {\bf R})} which agrees with {f} outside of a set of measure at most {\varepsilon}.

Proof: Observe that as {f} is finite everywhere, it is bounded outside of a set of arbitrarily small measure. Thus we may assume without loss of generality that {f} is bounded. Similarly, as {X} is {\sigma}-compact (or by inner regularity), the support of {f} differs from a compact set by a set of arbitrarily small measure; so we may assume that {f} is also supported on a compact set {K}. By Exercise 10, it then suffices to show that {f} is continuous on the complement of an open set of arbitrarily small measure; by outer regularity, we may delete the adjective "open" from the preceding sentence.

As {f} is bounded and compactly supported, {f} lies in {L^p(X,\mu)} for every {0 < p < \infty}, and using Proposition 3 and Chebyshev's inequality, it is not hard to find, for each {n = 1,2,\ldots}, a function {f_n \in C_c(X\rightarrow {\bf R})} which differs from {f} by at most {1/2^n} outside of a set of measure at most {\varepsilon/2^{n+2}} (say). In particular, {f_n} converges uniformly to {f} outside of a set of measure at most {\varepsilon/4}, and {f} is therefore continuous outside this set. The claim follows. \Box

Another very useful application of Urysohn's lemma is to create partitions of unity.

Lemma 6 (Partitions of unity) Let {X} be a normal topological space, and let {(K_\alpha)_{\alpha \in A}} be a collection of closed sets that cover {X}. For each {\alpha \in A}, let {U_\alpha} be an open neighbourhood of {K_\alpha}, which are finitely overlapping in the sense that each {x \in X} has a neighbourhood that intersects at most finitely many of the {U_\alpha}. Then there exists a continuous function {f_\alpha: X \rightarrow [0,1]} supported on {U_\alpha} for each {\alpha \in A} such that {\sum_{\alpha \in A} f_\alpha(x) = 1} for all {x \in X}.

If {X} is locally compact Hausdorff instead of normal, and the {K_\alpha} are compact, then one can take the {f_\alpha} to be compactly supported.

Proof: Suppose first that {X} is normal. By Urysohn's lemma, one can find a continuous function {g_\alpha: X \rightarrow [0,1]} for each {\alpha \in A} which is supported on {U_\alpha} and equals {1} on the closed set {K_\alpha}. Observe that the function {g := \sum_{\alpha \in A} g_\alpha} is well-defined, continuous and bounded below by {1}. The claim then follows by setting {f_\alpha := g_\alpha/g}.

The final claim follows by using Exercise 6 instead of Urysohn's lemma. \Box

Exercise 11 Let {X} be a topological space. A function {f: X \rightarrow {\bf R}} is said to be upper semi-continuous if {f^{-1}( (-\infty,a) )} is open for all real {a}, and lower semi-continuous if {f^{-1}( (a,+\infty) )} is open for all real {a}.

  1. Show that an indicator function {1_E} is upper semi-continuous if and only if {E} is closed, and lower semi-continuous if and only if {E} is open.
  2. If {X} is normal and Hausdorff, show that a function {f} is upper semi-continuous if and only if {f(x) = \inf\{ g(x): g \in C(X \rightarrow (-\infty,+\infty]), g \geq f \}} for all {x \in X}, and lower semi-continuous if and only if {f(x) = \sup\{ g(x): g \in C(X \rightarrow [-\infty,+\infty)), g \leq f \}} for all {x \in X}, where we write {f \leq g} if {f(x) \leq g(x)} for all {x \in X}.

— 2. The Riesz representation theorem —

Let {X} be a locally compact Hausdorff space which is also {\sigma}-compact. In Definition 2 we defined the notion of a Radon measure. Such measures are quite common in real analysis. For instance, we have the following result.

Theorem 7 Let {\mu} be a non-negative finite Borel measure on a compact metric space {X}. Then {\mu} is a Radon measure.

Proof: As {\mu} is finite, it is locally finite, so it suffices to show inner and outer regularity. Let {{\mathcal A}} be the collection of all Borel subsets {E} of {X} such that

\displaystyle \sup \{ \mu(K): K \subset E, \hbox{ closed} \} = \inf \{ \mu(U): U \supset E, \hbox{ op{}en} \} = \mu(E),

It will then suffice to show that every Borel set lies in {{\mathcal A}} (note that as {X} is compact, a subset {K} of {X} is closed if and only if it is compact).

Clearly {{\mathcal A}} contains the empty set and the whole set {X}, and is closed under complements. It is also closed under finite unions and intersections. Indeed, given two sets {E, F \in {\mathcal A}}, we can find a sequences {K_n \subset E \subset U_n}, {L_n \subset F \subset V_n} of closed sets {K_n, L_n} and open sets {U_n, V_n} such that {\mu(K_n), \mu(U_n) \rightarrow \mu(E)} and {\mu(L_n), \mu(V_n) \rightarrow \mu(F)}. Since

\displaystyle \mu(K_n \cap L_n) + \mu(K_n \cup L_n) = \mu(K_n) + \mu(L_n) \rightarrow \mu(E) + \mu(F) = \mu(E \cap F) + \mu(E \cup F)

we have (by monotonicity of {\mu}) that

\displaystyle \mu(K_n \cap L_n) \rightarrow \mu(E \cap F); \quad \mu(K_n \cup L_n) \rightarrow \mu(E \cup F)

and similarly

\displaystyle \mu(U_n \cap V_n) \rightarrow \mu(E \cap F); \quad \mu(U_n \cup V_n) \rightarrow \mu(E \cup F)

and so {E \cap F, E \cup F \in {\mathcal A}}.

One can also show that {{\mathcal A}} is closed under countable disjoint unions and is thus a {\sigma}-algebra. Indeed, given disjoint sets {E_n \in{\mathcal A}} and {\varepsilon > 0}, pick a closed {K_n \subset E_n} and open {U_n \supset E_n} such that {\mu(E_n \backslash K_n), \mu(U_n \backslash E_n) \leq \varepsilon/2^n}; then

\displaystyle \mu(\bigcup_{n=1}^\infty E_n) \leq \mu(\bigcup_{n=1}^\infty U_n) \leq \sum_{n=1}^\infty\mu(E_n) + \varepsilon

and

\displaystyle \mu(\bigcup_{n=1}^\infty E_n) \geq \mu(\bigcup_{n=1}^N K_n) \geq \sum_{n=1}^N \mu(E_n) - \varepsilon

for any {N}, and the claim follows from the squeeze test.

To finish the claim it suffices to show that every open set {V} lies in {{\mathcal A}}. For this it will suffice to show that {V} is a countable union of closed sets. But as {X} is a compact metric space, it is separable (Lemma 4 from Notes 10), and so {V} has a countable dense subset {x_1,x_2,\ldots}. One then easily verifies that every point in the open set {V} is contained in a closed ball of rational radius centred at one of the {x_i} that is in turn contained in {V}; thus {V} is the countable union of closed sets as desired. \Box

This result can be extended to more general spaces than compact metric spaces, for instance to Polish spaces (provided that the measure remains finite). For instance:

Exercise 12 Let {X} be a locally compact metric space which is {\sigma}-compact, and let {\mu} be an unsigned Borel measure which is finite on every compact set. Show that {\mu} is a Radon measure.

When the assumptions of {X} are weakened, then it is possible to find locally finite Borel measures that are not Radon measures, but they are somewhat pathological in nature.

Exercise 13 Let {X} be a locally compact Hausdorff space which is {\sigma}-compact, and let {\mu} be a Radon measure. Define a {F_\sigma} set to be a countable union of closed sets, and a {G_\delta} set to be a countable intersection of open sets. Show that every Borel set can be expressed as the union of an {F_\sigma} set and a null set, and as a {G_\delta} set with a null subset removed.

If {\mu} is a Radon measure on {X}, then we can define the integral {I_\mu(f) := \int_X f\ d\mu} for every {f \in C_c(X \rightarrow {\bf R})}, since {\mu} assigns every compact set a finite measure. Furthermore, {I_\mu} is a linear functional on {C_c(X \rightarrow {\bf R})} which is positive in the sense that {I_\mu(f) \geq 0} whenever {f} is non-negative. If we place the uniform norm on {C_c(X \rightarrow {\bf R})}, then {I_\mu} is continuous if and only if {\mu} is finite; but we will not use continuity for now, relying instead on positivity.

The fundamentally important Riesz representation theorem for such spaces asserts that this is the only way to generate such linear functionals:

Theorem 8 (Riesz representation theorem for {C_c(X \rightarrow {\bf R})}, unsigned version) Let {X} be a locally compact Hausdorff space which is also {\sigma}-compact. Let {I: C_c(X \rightarrow {\bf R}) \rightarrow {\bf R}} be a positive linear functional. Then there exists a unique Radon measure {\mu} on {X} such that {I = I_\mu}.

Remark 3 The {\sigma}-compactness hypothesis can be dropped (after relaxing the inner regularity condition to only apply to open sets, rather than to all sets); but I will restrict attention here to the {\sigma}-compact case (which already covers a large fraction of the applications of this theorem) as the argument simplifies slightly.

Proof: We first prove the uniqueness, which is quite easy due to all the properties that Radon measures enjoy. Suppose we had two Radon measures {\mu, \mu'} such that {I = I_\mu = I_{\mu'}}; in particular, we have

\displaystyle \int_X f\ d\mu = \int_X f\ d\mu' \ \ \ \ \ (1)

for all {f \in C_c(X \rightarrow {\bf R})}. Now let {K} be a compact set, and let {U} be an open neighbourhood of {K}. By Exercise 6, we can find {f \in C_c(X \rightarrow {\bf R})} with {1_K \leq f \leq 1_U}; applying this to (1), we conclude that

\displaystyle \mu(U) \geq \mu'(K).

Taking suprema in {K} and using inner regularity, we conclude that {\mu(U) \geq \mu'(U)}; exchanging {\mu} and {\mu'} we conclude that {\mu} and {\mu'} agree on open sets; by outer regularity we then conclude that {\mu} and {\mu'} agree on all Borel sets.

Now we prove existence, which is significantly trickier. We will initially make the simplifying assumption that {X} is compact (so in particular {C_c(X \rightarrow {\bf R}) = C(X \rightarrow {\bf R}) = BC(X \rightarrow {\bf R})}), and remove this assumption at the end of the proof.

Observe that {I} is monotone on {C(X \rightarrow {\bf R})}, thus {I(f) \leq I(g)} whenever {f \leq g}.

We would like to define the measure {\mu} on Borel sets {E} by defining {\mu(E) := I(1_E)}. This does not work directly, because {1_E} is not continuous. To get around this problem we shall begin by extending the functional {I} to the class {BC_{lsc}(X \rightarrow {\bf R}^+)} of bounded lower semi-continuous non-negative functions. We define {I(f)} for such functions by the formula

\displaystyle I(f) := \sup \{ I(g): g \in C_c(X \rightarrow {\bf R}); 0 \leq g \leq f \}

(cf. Exercise 11). This definition agrees with the existing definition of {I(f)} in the case when {f} is continuous. Since {I(1)} is finite and {I} is monotone, one sees that {I(f)} is finite (and non-negative) for all {f \in BC_{lsc}(X \rightarrow {\bf R}^+)}. One also easily sees that {I} is monotone on {BC_{lsc}(X \rightarrow {\bf R}^+)}: {I(f) \leq I(g)} whenever {f,g \in BC_{lsc}(X \rightarrow {\bf R}^+)} and {f \leq g}, and homogeneous in the sense that {I(cf) = cI(f)} for all {f \in BC_{lsc}(X \rightarrow {\bf R}^+)} and {c > 0}. It is also easy to verify the super-additivity property {I(f+f') \geq I(f) + I(f')} for {f, f' \in BC_{lsc}(X \rightarrow {\bf R}^+)}; this simply reflects the linearity of {I} on {C_c(X \rightarrow {\bf R})}, together with the fact that if {0 \leq g \leq f} and {0 \leq g' \leq f'}, then {0 \leq g+g' \leq f+f'}.

We now complement the super-additivity property with a countably sub-additive one: if {f_n \in BC_{lsc}(X \rightarrow {\bf R}^+)} is a sequence, and {f \in BC_{lsc}(X \rightarrow {\bf R}^+)} is such that {f(x) \leq \sum_{n=1}^\infty f_n(x)} for all {x \in X}, then {I(f) \leq \sum_{n=1}^\infty I(f_n)}.

Pick a small {0 < \varepsilon < 1}. It will suffice to show that {I(g) \leq \sum_{n=1}^\infty I(f_n) + O( \varepsilon^{1/2} )} (say) whenever {g \in C_c(X \rightarrow {\bf R})} is such that {0 \leq g \leq f}, and {O(\varepsilon^{1/2})} denotes a quantity bounded in magnitude by {C \varepsilon^{1/2}}, where {C} is a quantity that is independent of {\varepsilon}.

Fix {g}. For every {x \in X}, we can find a neighbourhood {U_x} of {x} such that {|g(y)-g(x)| \leq \varepsilon} for all {y \in U_x}; we can also find {N_x > 0} such that {\sum_{n=1}^{N_x} f_n(x) \geq f(x) - \varepsilon}. By shrinking {U_x} if necessary, we see from the lower semicontinuity of the {f_n} and {f} that we can also ensure that {f_n(y) \geq f_n(x) - \varepsilon/2^n} for all {1 \leq n \leq N_x} and {y \in U_x}.

By normality, we can find open neighbourhoods {V_x} of {x} whose closure lies in {U_x}. The {V_x} form an open cover of {X}. Since we are assuming {X} to be compact, we can thus find a finite subcover {V_{x_1},\ldots,V_{x_k}} of {X}. Applying Lemma 6, we can thus find a partition of unity {1 = \sum_{j=1}^k \psi_j}, where each {\psi_j} is supported on {U_{x_j}}.

Let {x \in X} be such that {g(x) \geq \sqrt{\varepsilon}}. Then we can write {g(x) = \sum_{j: x \in U_{x_j}} g(x) \psi_j(x)}. If {j} is in this sum, then {|g(x_j)-g(x)| \leq \varepsilon}, and thus (for {\varepsilon} small enough) {g(x_j) \geq \sqrt{\varepsilon}/2}, and hence {f(x_j) \geq \sqrt{\varepsilon}/2}. We can then write

\displaystyle 1 \leq \sum_{n=1}^{N_{x_j}} \frac{f_n(x_j)}{f(x_j)} + O( \sqrt{\varepsilon} )

and thus

\displaystyle g(x) \leq \sum_{n=1}^\infty \sum_{j: f(x_j) \geq \sqrt{\varepsilon}/2; N_{x_j} \geq n} \frac{f_n(x_j)}{f(x_j)} g(x_j) \psi_j(x) + O( \sqrt{\varepsilon} )

(here we use the fact that {\sum_j \psi_j(x)=1} and that the continuous compactly supported function {g} is bounded). Observe that only finitely many summands are non-zero. We conclude that

\displaystyle I(g) \leq \sum_{n=1}^\infty I (\sum_{j: f(x_j) \geq \sqrt{\varepsilon}/2; N_{x_j} \geq n} \frac{f_n(x_j)}{f(x_j)} g(x_j) \psi_j ) + O( \sqrt{\varepsilon} )

(here we use that {1 \in C_c(X)} and so {I(1)} is finite). On the other hand, for any {x \in X} and any {n}, the expression

\displaystyle \sum_{j: f(x_j) \geq \sqrt{\varepsilon}/2; N_{x_j} \geq n} \frac{f_n(x_j)}{f(x_j)} g(x_j) \psi_j(x)

is bounded from above by

\displaystyle \sum_j f_n(x_j) \psi_j(x);

since {f_n(x) \geq f_n(x_j) - \varepsilon/2^n} and {\sum_j \psi_j(x)=1}, this is bounded above in turn by

\displaystyle \varepsilon/2^n + f_n(x).

We conclude that

\displaystyle I(g) \leq \sum_{n=1}^\infty [I ( f_n ) + O( \varepsilon / 2^n )] + O( \sqrt{\varepsilon} )

and the sub-additivity claim follows.

Combining sub-additivity and super-additivity we see that {I} is additive: {I(f+g)=I(f)+I(g)} for {f, g \in BC_{lsc}(X \rightarrow {\bf R}^+)}.

Now that we are able to integrate lower semi-continuous functions, we can start defining the Radon measure {\mu}. When {U} is open, we define {\mu(U)} by

\displaystyle \mu(U) := I( 1_U ),

which is well-defined and non-negative since {1_U} is bounded, non-negative and lower semi-continuous. When {K} is closed we define {\mu(K)} by complementation:

\displaystyle \mu(K) := \mu(X) - \mu( X \backslash K );

this is compatible with the definition of {\mu} on open sets by additivity of {I}, and is also non-negative. The monotonicity of {I} implies monotonicity of {\mu}: in particular, if a closed set {K} lies in an open set {U}, then {\mu(K) \leq \mu(U)}.

Given any set {E \subset X}, define the outer measure

\displaystyle \mu^+(E) := \inf \{ \mu(U): E \subset U, \hbox{ op{}en} \}

and the inner measure

\displaystyle \mu^-(E) := \sup \{ \mu(K): E \supset K, \hbox{ closed} \};

thus {0 \leq \mu^-(E) \leq \mu^+(E) \leq \mu(X)}. We call a set {E} measurable if {\mu^-(E) = \mu^+(E)}. By arguing as in the proof of Theorem 7, we see that the class of measurable sets is a Boolean algebra. Next, we claim that every open set {U} is measurable. Indeed, unwrapping all the definitions we see that

\displaystyle \mu(U) = \sup \{ I(f): f \in C_c(X \rightarrow {\bf R}); 0 \leq f \leq 1_U \}.

Each {f} in this supremum is supported in some closed subset {K} of {U}, and from this one easily verifies that {\mu^+(U) = \mu(U) = \mu^-(U)}. Similarly, every closed set {K} is measurable. We can now extend {\mu} to measurable sets by declaring {\mu(E) := \mu^+(E) = \mu^-(E)} when {E} is measurable; this is compatible with the previous definitions of {\mu}.

Next, let {E_1, E_2, \ldots} be a countable sequence of disjoint measurable sets. Then for any {\epsilon > 0}, we can find open neighbourhoods {U_n} of {E_n} and closed sets {K_n} in {E_n} such that {\mu(E_n) \leq \mu(U_n) \leq \mu(E_n) + \epsilon/2^n} and {\mu(E_n)-\epsilon/2^n \leq \mu(K_n) \leq \mu(E_n)}. Using the sub-additivity of {I} on {BC_{lsc}(X \rightarrow {\bf R}^+)}, we have {\mu(\bigcup_{n=1}^\infty U_n) \leq \sum_{n=1}^\infty \mu(U_n) \leq \sum_{n=1}^\infty \mu(E_n) + \varepsilon}. Similarly, from the additivity of {I} we have {\mu(\bigcup_{n=1}^N K_n) = \sum_{n=1}^N \mu(K_n) \geq \sum_{n=1}^N \mu(E_n) - \varepsilon}. Letting {\varepsilon \rightarrow 0}, we conclude that {\bigcup_{n=1}^\infty E_n} is measurable with {\mu( \bigcup_{n=1}^\infty E_n ) = \sum_{n=1}^\infty \mu(E_n)}. Thus the Boolean algebra of measurable sets is in fact a {\sigma}-algebra, and {\mu} is a countably additive measure on it. From construction we also see that it is finite, outer regular, and inner regular, and therefore is a Radon measure. The only remaining thing to check is that {I(f) = I_\mu(f)} for all {f \in C(X \rightarrow {\bf R})}. If {f} is a finite non-negative linear combination of indicator functions of open sets, the claim is clear from the construction of {\mu} and the additivity of {I} on {BC_{lsc}(X \rightarrow {\bf R}^+)}; taking uniform limits, we obtain the claim for non-negative continuous functions, and then by linearity we obtain it for all functions.

This concludes the proof in the case when {X} is compact. Now suppose that {X} is {\sigma}-compact. Then we can find a partition of unity {1 = \sum_{n=0}^\infty \psi_n} into continuous compactly supported functions {\psi_n \in C_c(X \rightarrow {\bf R}^+)}, with each {x \in X} being contained in the support of finitely many {\psi_n}. (Indeed, from {\sigma}-compactness and the locally compact Hausdorff property one can find a nested sequence {K_1 \subset K_2 \subset \ldots} of compact sets, with each {K_n} in the interior of {K_{n+1}}, such that {\bigcup_n K_n = X}. Using Exercise 6, one can find functions {\eta_n \in C_c(X \rightarrow {\bf R}^+)} that equal {1} on {K_n} and are supported on {K_{n+1}}; now take {\psi_n := \eta_{n+1} - \eta_n} and {\psi_0 := \eta_0}.) Observe that {I(f) = \sum_n I(\psi_n f)} for all {f \in C_c(X \rightarrow {\bf R})}. From the compact case we see that there exists a finite Radon measure {\mu_n} such that {I(\psi_n f) = I_{\mu_n}(f)} for all {f \in C_c(X \rightarrow {\bf R})}; setting {\mu := \sum_n \mu_n} one can verify (using the monotone convergence theorem) that {\mu} obeys the required properties. \Box

Remark 4 One can also construct the Radon measure {\mu} using the Carátheodory extension theorem; this proof of the Riesz representation theorem can be found in many real analysis texts. A third method is to first create the space {L^1} by taking the completion of {C_c(X \rightarrow {\bf R})} with respect to the {L^1} norm {\| f \|_{L^1} := I(|f|)}, and then define {\mu(E) := \| 1_E \|_{L^1}}. It seems to me that all three proofs are about equally lengthy, and ultimately rely on the same ingredients; they all seem to have their strengths and weaknesses, and involve at least one tricky computation somewhere (in the above argument, the most tricky thing is the countable subadditivity of {I} on lower semicontinuous functions). I have yet to find a proof of this theorem which is both clean and conceptual, and would be happy to learn of other proofs of this theorem.

Remark 5 One can use the Riesz representation theorem to provide an alternate construction of Lebesgue measure, say on {{\bf R}}. Indeed, the Riemann integral already provides a positive linear functional on {C_c({\bf R} \rightarrow {\bf R})}, which by the Riesz representation theorem must come from a Radon measure, which can be easily verified to assign the value {b-a} to every interval {[a,b]} and thus must agree with Lebesgue measure. The same approach lets one define volume measures on manifolds with a volume form.

Exercise 14 Let {X} be a locally compact Hausdorff space which is {\sigma}-compact, and let {\mu} be a Radon measure. For any non-negative Borel measurable function {f}, show that

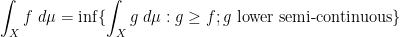
\displaystyle \int_X f\ d\mu = \inf \{ \int_X g\ d\mu: g \geq f; g \hbox{ lower semi-continuous} \}

and

\displaystyle \int_X f\ d\mu = \sup \{ \int_X g\ d\mu: 0 \leq g \leq f; g \hbox{ upper semi-continuous} \}.

Similarly, for any non-negative lower semi-continuous function {g}, show that

\displaystyle \int_X g\ d\mu = \sup \{ \int_X h\ d\mu: 0 \leq h \leq g; h \in C_c(X \rightarrow {\bf R}) \}.

Now we consider signed functionals on {C_c(X \rightarrow {\bf R})}, which we now turn into a normed vector space using the uniform norm. The key lemma here is the following variant of the Jordan decomposition theorem.

Lemma 9 (Jordan decomposition for functions) Let {I \in C_c(X \rightarrow {\bf R})^*} be a (real) continuous linear functional. Then there exist positive linear functions {I^+, I^- \in C_c(X \rightarrow {\bf R})^*} such that {I = I^+ - I^-}.

Proof: For {f \in C_c(X \rightarrow {\bf R}^+)}, we define

\displaystyle I^+(f) := \sup \{ I(g): g \in C_c(X \rightarrow {\bf R}): 0 \leq g \leq f \}.

Clearly {0 \leq I(f) \leq I^+(f)} for {f \in C_c(X \rightarrow {\bf R}^+)}; one also easily verifies the homogeneity property {I^+(cf) = c I^+(f)} and super-additivity property {I^+(f_1+f_2) \geq I^+(f_1)+I^+(f_2)} for {c>0} and {f, f_1, f_2 \in C_c(X \rightarrow {\bf R}^+)}. On the other hand, if {g, f_1, f_2 \in C_c(X \rightarrow {\bf R}^+)} are such that {g \leq f_1+f_2}, then we can decompose {g = g_1+g_2} for some {g_1, g_2 \in C_c(X \rightarrow {\bf R}^+)} with {g_1 \leq f_1} and {g_2 \leq f_2}; for instance we can take {g_1 := \min(g,f_1)} and {g_2 := g-g_1}. From this we can complement super-additivity with sub-additivity and conclude that {I^+(f_1+f_2) = I^+(f_1)+I^+(f_2)}.

Every function in {C_c(X \rightarrow {\bf R})} can be expressed as the difference of two functions in {C_c(X \rightarrow {\bf R}^+)}. From the additivity and homogeneity of {I^+} on {C_c(X \rightarrow {\bf R}^+)} we may thus extend {I^+} uniquely to be a linear functional on {C_c(X \rightarrow {\bf R})}. Since {I} is bounded on {C_c(X \rightarrow {\bf R})}, we see that {I^+} is also. If we then define {I^- := I^+ - I}, one quickly verifies all the required properties. \Box

Exercise 15 Show that among all possible choices for the functionals {I^+, I^-} appearing in the above lemma, there is a unique choice which is minimal in the sense that for any other functionals {\tilde I^+, \tilde I^-} obeying the conclusions of the lemma, one has {\tilde I^+(f) \geq I^+(f)} and {\tilde I^-(f) \geq I^-(f)} for all nonnegative {f \in C_c(X \rightarrow {\bf R})}.

Define a signed Radon measure on a {\sigma}-compact, locally compact Hausdorff space {X} to be a signed Borel measure {\mu} whose positive and negative variations are both Radon. It is easy to see that a signed Radon measure {\mu} generates a linear functional {I_\mu} on {C_c(X \rightarrow {\bf R})} as before, and {I_\mu} is continuous if {\mu} is finite. We have a converse:

Exercise 16 (Riesz representation theorem, signed version) Let {X} be a locally compact Hausdorff space which is also {\sigma}-compact, and let {I \in C_c(X \rightarrow {\bf R})^*} be a continuous linear functional. Then there exists a unique signed finite Radon measure {\mu} such that {I = I_\mu}. (Hint: combine Theorem 8 with Lemma 9.)

The space of signed finite Radon measures on {X} is denoted {M(X \rightarrow {\bf R})}, or {M(X)} for short.

Exercise 17 Show that the space {M(X)}, with the total variation norm {\| \mu \|_{M(X)} := |\mu|(X)}, is a real Banach space, which is isomorphic to the dual of both {C_c(X \rightarrow {\bf R})} and its completion {C_0(X \rightarrow {\bf R})}, thus

\displaystyle C_c(X \rightarrow {\bf R})^* \equiv C_0(X \rightarrow {\bf R})^* \equiv M(X).

Remark 6 Note that the previous exercise generalises the identifications {c_c({\bf N})^* \equiv c_0({\bf N})^* \equiv \ell^1({\bf N})} from previous notes. For compact Hausdorff spaces {X}, we have {C(X \rightarrow {\bf R}) = C_0(X \rightarrow {\bf R})}, and thus {C(X \rightarrow {\bf R})^* \equiv M(X)}. For locally compact Hausdorff spaces that are {\sigma}-compact but not compact, we instead have {C(X \rightarrow {\bf R})^* \equiv M(\beta X)}, where {\beta X} is the Stone-Cech compactification of {X}, which we will discuss in later notes.

Remark 7 One can of course also define complex Radon measures to be those complex finite Borel measures whose real and imaginary parts are signed Radon measures, and define {M(X \rightarrow {\bf C})} to be the space of all such measures; then one has analogues of the above identifications. We omit the details.

Exercise 18 Let {X, Y} be two locally compact Hausdorff spaces that are also {\sigma}-compact, and let {f: X \rightarrow Y} be a continuous map. If {\mu} is an unsigned finite Radon measure on {X}, show that the pushforward measure {f_\# \mu} on {Y}, defined by {f_\# \mu(E) := \mu(f^{-1}(E))}, is a Radon measure on {Y}. What happens for infinite measures? Establish the same fact for signed finite Radon measures.

Let {X} be locally compact Hausdorff and {\sigma}-compact. As {M(X)} is equivalent to the dual of the Banach space {C_0(X \rightarrow {\bf R})}, it acquires a weak* topology (see Notes 11), known as the vague topology. A sequence of Radon measures {\mu_n \in M(X)} then converges vaguely to a limit {\mu \in M(X)} if and only if {\int_X f\ d\mu_n \rightarrow \int_X f\ d\mu} for all {f \in C_0(X \rightarrow {\bf R})}.

Exercise 19 Let {m} be Lebesgue measure on the real line (with the usual topology).

Exercise 20 Let {X} be locally compact Hausdorff and {\sigma}-compact. Show that for every unsigned Radon measure {\mu}, the map {\iota: L^1(\mu) \rightarrow M(X)} defined by sending {f \in L^1(\mu)} to the measure {\mu_f} is an isometry, thus {L^1(\mu)} can be identified with a subspace of {M(X)}. Show that this subspace is closed in the norm topology, but give an example to show that it need not be closed in the vague topology. Show that {M(X) = \bigcup_\mu L^1(\mu)}, where {\mu} ranges over all unsigned Radon measures on {X}; thus one can think of {M(X)} as many {L^1}'s "glued together".

Exercise 21 Let {X} be a locally compact Hausdorff space which is {\sigma}-compact. Let {f_n \in C_0(X \rightarrow {\bf R})} be a sequence of functions, and let {f \in C_0(X \rightarrow {\bf R})} be another function. Show that {f_n} converges weakly to {f} in {C_0(X \rightarrow {\bf R})} if and only if the {f_n} are uniformly bounded and converge pointwise to {f}.

Exercise 22 Let {X} be a locally compact metric space which is {\sigma}-compact.

— 3. The Stone-Weierstrass theorem —

We have already seen how rough functions (e.g. {L^p} functions) can be approximated by continuous functions. Now we study in turn how continuous functions can be approximated by even more special functions, such as polynomials. The natural topology to work with here is the uniform topology (since uniform limits of continuous functions are continuous).

For non-compact spaces, such as {{\bf R}}, it is usually not possible to approximate continuous functions uniformly by a smaller class of functions. For instance, the function {\sin(x)} cannot be approximated uniformly by polynomials on {{\bf R}}, since {\sin(x)} is bounded, the only bounded polynomials are the constants, and constants cannot converge to anything other than another constant. On the other hand, on a compact domain such as {[-1,1]}, one can easily approximate {\sin(x)} uniformly by polynomials, for instance by using Taylor series. So we will focus instead on compact Hausdorff spaces {X} such as {[-1,1]}, in which continuous functions are automatically bounded.

The space {{\mathcal P}([-1,1])} of (real-valued) polynomials is a subspace of the Banach space {C([-1,1])}. But it is also closed under pointwise multiplication {f, g\mapsto fg}, making {{\mathcal P}([-1,1])} an algebra, and not merely a vector space. We can then rephrase the classical Weierstrass approximation theorem as the assertion that {{\mathcal P}([-1,1])} is dense in {C([-1,1])}.

One can then ask the more general question of when a sub-algebra {{\mathcal A}} of {C(X)} – i.e. a subspace closed under pointwise multiplication – is dense. Not every sub-algebra is dense: the algebra of constants, for instance, will not be dense in {C(X)} when {X} has at least two points. Another example in a similar spirit: given two distinct points {x_1, x_2} in {X}, the space {\{ f \in C(X): f(x_1) = f(x_2) \}} is a sub-algebra of {C(X)}, but it is not dense, because it is already closed, and cannot separate {x_1} and {x_2} in the sense that it cannot produce a function that assigns different values to {x_1} and {x_2}.

The remarkable Stone-Weierstrass theorem shows that this inability to separate points is the only obstruction to density, at least for algebras with the identity.

Theorem 10 (Stone-Weierstrass theorem, real version) Let {X} be a compact Hausdorff space, and let {{\mathcal A}} be a sub-algebra of {C(X \rightarrow {\bf R})} which contains the constant function {1} and separates points (i.e. for every distinct {x_1, x_2 \in X}, there exists at least one {f} in {{\mathcal A}} such that {f(x_1) \neq f(x_2)}. Then {{\mathcal A}} is dense in {C(X \rightarrow {\bf R})}.

Remark 8 Observe that this theorem contains the Weierstrass approximation theorem as a special case, since the algebra of polynomials clearly separates points. Indeed, we will use (a very special case) of the Weierstrass approximation theorem in the proof.

Proof: It suffices to verify the claim for algebras {{\mathcal A}} which are closed in the {C(X \rightarrow {\bf R})} topology, since the claim follows in the general case by replacing {{\mathcal A}} with its closure (note that the closure of an algebra is still an algebra).

Observe from the Weierstrass approximation theorem that on any bounded interval {[-K,K]}, the function {|x|} can be expressed as the uniform limit of polynomials {P_n(x)}; one can even write down explicit formulae for such a {P_n}, though we will not need such formulae here. Since continuous functions on the compact space {X} are bounded, this implies that for any {f \in {\mathcal A}}, the function {|f|} is the uniform limit of polynomial combinations {P_n(f)} of {f}. As {{\mathcal A}} is an algebra, the {P_n(f)} lie in {{\mathcal A}}; as {{\mathcal A}} is closed; we see that {|f|} lies in {{\mathcal A}}.

Using the identities {\max(f,g) = \frac{f+g}{2} + |\frac{f-g}{2}|}, {\min(f,g) = \frac{f+g}{2} - |\frac{f-g}{2}|}, we conclude that {{\mathcal A}} is a lattice in the sense that one has {\max(f,g), \min(f,g) \in {\mathcal A}} whenever {f, g \in {\mathcal A}}.

Now let {f \in C(X \rightarrow {\bf R})} and {\varepsilon > 0}. We would like to find {g \in {\mathcal A}} such that {|f(x)-g(x)| \leq \varepsilon} for all {x \in X}.

Given any two points {x, y \in X}, we can at least find a function {g_{xy} \in {\mathcal A}} such that {g_{xy}(x)=f(x)} and {g_{xy}(y)=f(y)}; this follows since the vector space {{\mathcal A}} separates points and also contains the identity function (the case {x=y} needs to be treated separately). We now use these functions {g_{xy}} to build the approximant {g}. First, observe from continuity that for every {x, y \in X} there exists an open neighbourhood {V_{xy}} of {y} such that {g_{xy}(y') \geq f(y')-\varepsilon} for all {y' \in V_{xy}}. By compactness, for any fixed {x} we can cover {X} by a finite number of these {V_{xy}}. Taking the max of all the {g_{xy}} associated to this finite subcover, we create another function {g_x \in {\mathcal A}} such that {g_x(x) = f(x)} and {g_x(y) \geq f(y) - \varepsilon} for all {y \in X}. By continuity, we can find an open neighbourhood {U_x} of {x} such that {g_x(x') \leq f(x')+\varepsilon} for all {x' \in U_x}. Again applying compactness, we can cover {X} by a finite number of the {U_x}; taking the min of all the {g_x} associated to this finite subcover we obtain {g \in {\mathcal A}} with {f(x)-\varepsilon \leq g(x) \leq f(x)+\varepsilon} for all {x \in X}, and the claim follows. \Box

There is an analogue of the Stone-Weierstrass theorem for algebras that do not contain the identity:

Exercise 23 Let {X} be a compact Hausdorff space, and let {{\mathcal A}} be a closed sub-algebra of {C(X \rightarrow {\bf R})} which separates points but does not contain the identity. Show that there exists a unique {x_0 \in X} such that {{\mathcal A} = \{ f \in C(X \rightarrow {\bf R}): f(x_0)=0 \}}.

The Stone-Weierstrass theorem is not true as stated in the complex case. For instance, the space {C( \mathbb{D} \rightarrow {\bf C} )} of complex-valued functions on the closed unit disk {\mathbb{D} := \{ z \in {\bf C}: |z| \leq 1 \}} has a closed proper sub-algebra that separates points, namely the algebra {{\mathcal H}({\mathbb D})} of functions in {C( \mathbb{D} \rightarrow {\bf C} )} that are holomorphic on the interior of this disk. Indeed, by Cauchy's theorem and its converse (Morera's theorem), a function {f \in C(\mathbb{D} \rightarrow {\bf C})} lies in {{\mathcal H}({\mathbb D})} if and only if {\int_\gamma f = 0} for every closed contour {\gamma} in {{\mathbb D}}, and one easily verifies that this implies that {{\mathcal H}({\mathbb D})} is closed; meanwhile, the holomorphic function {z \mapsto z} separates all points. However, the Stone-Weierstrass theorem can be recovered in the complex case by adding one further axiom, namely that the algebra be closed under conjugation:

Exercise 24 (Stone-Weierstrass theorem, complex version) Let {X} be a compact Hausdorff space, and let {{\mathcal A}} be a complex sub-algebra of {C(X \rightarrow {\bf C})} which contains the constant function {1}, separates points, and is closed under the conjugation operation {f \mapsto \overline{f}}. Then {{\mathcal A}} is dense in {C(X \rightarrow {\bf C})}.

Exercise 25 Let {{\mathcal T} \subset C({\bf R}/{\bf Z} \rightarrow {\bf C})} be the space of trigonometric polynomials {x \mapsto \sum_{n=-N}^N c_n e^{2\pi i n x}} on the unit circle {{\bf R}/{\bf Z}}, where {N \geq 0} and the {c_n} are complex numbers. Show that {{\mathcal T}} is dense in {C({\bf R}/{\bf Z} \rightarrow {\bf C})} (with the uniform topology), and that {{\mathcal T}} is dense in {L^p({\bf R}/{\bf Z} \rightarrow {\bf C})} (with the {L^p} topology) for all {0 < p < \infty}.

Exercise 26 Let {X} be a locally compact Hausdorff space that is {\sigma}-compact, and let {{\mathcal A}} be a sub-algebra of {C(X \rightarrow {\bf R})} which separates points and contains the identity function. Show that for every function {f \in C(X \rightarrow {\bf R})} there exists a sequence {f_n \in {\mathcal A}} which converges to {f} uniformly on compact subsets of {X}.

Exercise 27 Let {X, Y} be compact Hausdorff spaces. Show that every function {f \in C( X \times Y \rightarrow {\bf R})} can be expressed as the uniform limit of functions of the form {(x,y) \mapsto \sum_{j=1}^k f_j(x) g_j(y)}, where {f_j \in C(X \rightarrow {\bf R})} and {g_j \in C(Y \rightarrow {\bf R})}.

Exercise 28 Let {(X_\alpha)_{\alpha \in A}} be a family of compact Hausdorff spaces, and let {X := \prod_{\alpha \in A} X_\alpha} be the product space (with the product topology). Let {f \in C(X \rightarrow {\bf R})}. Show that {f} can be expressed as the uniform limit of continuous functions {f_n}, each of which only depend on finitely many of the coordinates in {A}, thus there exists a finite subset {A_n} of {A} and a continuous function {g_n \in C(\prod_{\alpha \in A_n} X_\alpha \rightarrow {\bf R})} such that {f_n( (x_\alpha)_{\alpha \in A} ) = g_n( (x_\alpha)_{\alpha \in A_n} )} for all {(x_\alpha)_{\alpha \in A} \in X}.

One useful application of the Stone-Weierstrass theorem is to demonstrate separability of spaces such as {C(X)}.

Proposition 11 Let {X} be a compact metric space. Then {C(X \rightarrow {\bf C})} and {C(X \rightarrow {\bf R})} are separable.

Proof: It suffices to show that {C(X \rightarrow {\bf R})} is separable. By Lemma 4 of Notes 10, {X} has a countable dense subset {x_1,x_2,\ldots}. By Urysohn's lemma, for each {n, m \geq 1} we can find a function {\psi_{n,m} \in C(X \rightarrow {\bf R})} which equals {1} on {B(x_n,1/m)} and is supported on {B(x_n,2/m)}. The {\psi_{n,m}} can then easily be verified to separate points, and so by the Stone-Weierstrass theorem, the algebra of polynomial combinations of the {\psi_{n,m}} in {C(X \rightarrow {\bf R})} are dense; this implies that the algebra of rational polynomial combinations of the {\psi_{n,m}} are dense, and the claim follows. \Box

Combining this with the Riesz representation theorem and the sequential Banach-Alaoglu theorem, we obtain

Corollary 12 If {X} is a compact metric space, then the closed unit ball of {M(X)} is sequentially compact in the vague topology.

Combining this with Theorem 7, we conclude a special case of Prokhorov's theorem:

Corollary 13 (Prokhorov's theorem, compact case) Let {X} be a compact metric space, and let {\mu_n} be a sequence of Borel (hence Radon) probability measures on {X}. Then there exists a subsequence of {\mu_n} which converge vaguely to another Borel probability measure {\mu}.

Exercise 29 (Prokhorov's theorem, non-compact case) Let {X} be a locally compact metric space which is {\sigma}-compact, and let {\mu_n} be a sequence of Borel probability measures. We assume that the sequence {\mu_n} is tight, which means that for every {\varepsilon > 0} there exists a compact set {K} such that {\mu_n(X \backslash K) \leq \varepsilon} for all {n}. Show that there is a subsequence of {\mu_n} which converges vaguely to another Borel probability measure {\mu}. If tightness is not assumed, show that there is a subsequence which converges vaguely to a non-negative Borel measure {\mu}, but give an example to show that this measure need not be a probability measure.

This theorem can be used to establish Helly's selection theorem:

Exercise 30 (Helly's selection theorem) Let {f_n: {\bf R} \rightarrow {\bf R}} be a sequence of functions whose total variation is uniformly bounded in {n}, and which is bounded at one point {x_0 \in {\bf R}} (i.e. {\{ f_n(x_0): n=1,2,\ldots\}} is bounded). Show that there exists a subsequence of {f_n} which converges pointwise almost everywhere on compact subsets of {{\bf R}}. (Hint: one can deduce this from Prokhorov's theorem using the fundamental theorem of calculus for functions of bounded variation.)

— 4. The commutative Gelfand-Naimark theorem (optional) —

One particularly beautiful application of the machinery developed in the last few notes is the commutative Gelfand-Naimark theorem, that classifies commutative {C^*}-algebras, and is of importance in spectral theory, operator algebras, and quantum mechanics.

Definition 14 A complex Banach algebra is a complex Banach space {A} which is also a complex algebra, such that {\|xy\| \leq \|x\| \|y\|} for all {x,y \in A}. An algebra is unital if it contains a multiplicative identity {1}, and commutative if {xy=yx} for all {x,y \in A}. A {C^*}-algebra is a complex Banach algebra with an anti-homomorphism map {x \mapsto x^*} from {A} to {A} (thus {(xy)^* = y^* x^*}, {(x+y)^*=x^*+y^*}, and {(cx)^* = \overline{c} x} for {x,y \in A} and {c \in {\bf C}}) which is an isometry (thus {\|x^*\|=\|x\|} for all {x \in A}), an involution (thus {(x^*)^*=x} for all {x \in A}), and obeys the {C^*} identity {\|x^* x \| = \|x\|^2} for all {x \in A}.

A homomorphism {\phi: A \rightarrow B} between two {C^*}-algebras is a continuous algebra homomorphism such that {\phi(x^*) =\phi(x)^*} for all {x \in X}. An isomorphism is an homomorphism whose inverse exists and is also a homomorphism; two {C^*}-algebras are isomorphic if there exists an isomorphism between them.

Exercise 31 If {H} is a Hilbert space, and {B(H \rightarrow H)} is the algebra of bounded linear operators on this space, with the adjoint map {T \mapsto T^*} and the operator norm, show that {B(H \rightarrow H)} is a unital {C^*}-algebra (not necessarily commutative). Indeed, one can think of {C^*}-algebras as an abstraction of a space of bounded linear operators on a Hilbert space (this is basically the content of the non-commutative Gelfand-Naimark theorem, which we will not discuss here).

Exercise 32 If {X} is a compact Hausdorff space, show that {C(X \rightarrow {\bf C})} is a unital commutative {C^*}-algebra, with involution {f^* := \overline{f}}.

The remarkable (unital commutative) Gelfand-Naimark theorem asserts the converse statement to Exercise 32:

Theorem 15 (Unital commutative Gelfand-Naimark theorem) Every unital commutative {C^*}-algebra {A} is isomorphic to {C(X \rightarrow {\bf C})} for some compact Hausdorff space {X}.

There are analogues of this theorem for non-unital or non-commutative {C^*}-algebras, but for simplicity we shall restrict attention to the unital commutative case. We first need some spectral theory.

Exercise 33 Let {A} be a unital Banach algebra. Show that if {x \in A} is such that {\|x-1\|<1}, then {x} is invertible. (Hint: use Neumann series.) Conclude that the space {A^\times \subset A} of invertible elements of {A} is open.

Define the spectrum {\sigma(x)} of an element {x \in A} to be the set of all {z \in {\bf C}} such that {x - z 1} is not invertible.

Exercise 34 If {A} is a unital Banach algebra and {x \in A}, show that {\sigma(x)} is a compact subset of {{\bf C}} that is contained inside the disk {\{ z \in {\bf C}: |z| \leq \|x\| \}}.

Exercise 35 (Beurling-Gelfand spectral radius formula) If {A} is a unital Banach algebra and {x \in A}, show that {\sigma(x)} is non-empty with {\sup \{ |z|: z \in \sigma(x) \} = \lim_{n \rightarrow \infty} \|x^n\|^{1/n}}. (Hint: To get the upper bound, observe that if {x^n-z^n1} is invertible for some {n \geq 1}, then so is {x-zI}, then use Exercise 34. To get the lower bound, first observe that for any {\lambda \in A^*}, the function {f_\lambda: z \mapsto \lambda( (x-zI)^{-1} )} is holomorphic on the complement of {\sigma(x)}, which is already enough (with Liouville's theorem) to show that {\sigma} is non-empty. Let {r > \sup \{ |z|: z \in \sigma(x) \}} be arbitrary, then use Laurent series to show that {|\lambda( x^n )| \leq C_{\lambda,r} r^n} for all {n} and some {C_{\lambda,r}} independent of {n}. Then divide by {r^n} and use the uniform boundedness principle to conclude.)

Exercise 36 ({C^*}-algebra spectral radius formula) Let {A} be a unital {C^*}-algebra. Show that

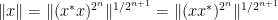
\displaystyle \|x \| = \| (x^* x)^{2^n} \|^{1/2^{n+1}} = \| (x x^*)^{2^n} \|^{1/2^{n+1}}

for all {n \geq 1} and {x \in A}. Conclude that any homomorphism between {C^*}-algebras has operator norm at most {1}. Also conclude that

\displaystyle \sup \{ |z|: z \in \sigma(x) \} = \|x\|

when {x} is self-adjoint.

The next important concept is that of a character.

Definition 16 Let {A} be a unital commutative {C^*}-algebra. A character of {A} is be an element {\lambda \in A^*} in the dual Banach space such that {\lambda(xy) = \lambda(x)\lambda(y)}, {\lambda(1)=1}, and {\lambda(x^*) = \overline{\lambda(x)}} for all {x,y \in A}; equivalently, a character is a homomorphism from {A} to {{\bf C}} (viewed as a (unital) {C^*} algebra). We let {\hat A \subset A^*} be the space of all characters; this space is known as the spectrum of {A}.

Exercise 37 If {A} is a unital commutative {C^*}-algebra, show that {\hat A} is a compact Hausdorff subset of {A^*} in the weak-* topology. (Hint: first use the spectral radius formula to show that all characters have operator norm {1}, then use the Banach-Alaoglu theorem.)

Exercise 38 Define an ideal of a unital commutative {C^*}-algebra {A} to be a proper subspace {I} of {A} such that {xy, yx \in I} for all {x \in I} and {y \in A}. Show that if {\lambda \in \hat A}, then the kernel {\lambda^{-1}(\{0\})} is a maximal ideal in {A}; conversely, if {I} is a maximal ideal in {A}, show that {I} is closed, and there is exactly one {\lambda \in \hat A} such that {I = \lambda^{-1}(\{0\})}. Thus the spectrum of {A} can be canonically identified with the space of maximal ideals in {A}.

Exercise 39 Let {X} be a compact Hausdorff space, and let {A} be the {C^*}-algebra {A := C(X \rightarrow {\bf C})}. Show that for each {x \in X}, the operation {\lambda_x: f \mapsto f(x)} is a character of {A}. Show that the map {\lambda: x \mapsto \lambda_x} is a homeomorphism from {X} to {\hat A}; thus the spectrum of {C(X \rightarrow {\bf C})} can be canonically identified with {X}. (Hint: use Exercise 23 to show the surjectivity of {\lambda}, Urysohn's lemma to show injectivity, and Corollary 2 of Notes 10 to show the homeomorphism property.)

Inspired by the above exercise, we define the Gelfand representation {\hat{}: A \mapsto C(\hat A \rightarrow {\bf C})}, by the formula {\hat x(\lambda) := \lambda(x)}.

Exercise 40 Show that if {A} is a unital commutative {C^*}-algebra, then the Gelfand representation is a homomorphism of {C^*}-algebras.

Exercise 41 Let {x} be a non-invertible element of a unital commutative {C^*}-algebra {A}. Show that {\hat x} vanishes at some {\lambda \in \hat A}. (Hint: the set {\{ xy: y \in A \}} is a proper ideal of {A}, and thus by Zorn's lemma is contained in a maximal ideal.)

Exercise 42 Show that if {A} is a unital commutative {C^*}-algebra, then the Gelfand representation is an isometry. (Hint: use Exercise 36 and Exercise 41.)

Exercise 43 Use the complex Stone-Weierstrass theorem and Exercises 40, 42 to conclude the proof of Theorem 15.